Why and What is liblb?
It all started when a friend of mine complained about how the load balancing algorithm he was using wasn't delivering the outcomes he was expecting. Because of his somewhat unique use case I was very intrigued, so I decided to help him solve the issue. Not long after, I found myself researching the literature on all the load balancing algorithms I could find. After a while, I decided to build a this simulation to better evaluate the algorithms based on:
- Algorithm simplicity
- Load distribution
- Affinity and cache friendliness
- The guarantees provided
Each algorithm serves a particular use case on a different side of the spectrum. Which should cater to most applications, ranging from CDNs to CRUD applications that keep their state in a centralized database.
Comparison
| Algorithm | Load Distribution | Cache Friendliness | Guarantees |
|---|---|---|---|
| Round-Robin | Uniform load distribution, if the requests take the same time. | Not friendly, because it assigns work to hosts randomly. | All hosts will get the same number of requests. |
| Two Random Choices | Max load of any server is O(log log number_of_servers). |
Not friendly, because it assigns work to hosts randomly. | Host's max load will be O(log log number_of_servers), with high probability. |
| Consistent Hashing | Load distribution is skewed, due to the random slicing of the ring. | Very friendly, because it'll always assign the same key to the same host, unless the topology changes. | When the topology changes, only 1/number_of_server will be assigned to different hosts. |
| Bounded Consistent Hashing | Max Load of a host will never exceed ceil(average_load*scale_factor). |
Very Friendly, unless a host load reaches its max, then it'll distribute requests coming to it to other hosts. | Adding or removing a host changes location of 1/(e^2) where e is scale_factor-1 - e in our case is 0.25-. |
Simulation
The simulation is derived from a day's worth of anonymized real traffic logs donated from a major Online Classifieds site in the Middle East, which makes the study more meaningful than a randomly generated traffic.
before explaining the simulation let's talk about its Components:
- Client: a user that asks for the country of a certain IP. It sends the request to one of the GeoServer hosts given to it by consulting liblb
- GeoServer Host: responds the incoming queries by returning the country of the given IP either from its local Cache if found, or directly from the database.
Now that we got this out of the way, let's see how the simulation works:
- Client: Extracts the user's IP from the logs.
- Client: Sends the IP to the GeoServer host the liblb gave it (for example) based on the selected algorithm.
- GeoServer Host: Looks in its in-memory cache, if found it increments a cache hit counter and return the cached result.
- GeoServer Host: If the IP is not found in the cache, the GeoServer Host increments a cache miss counter and returns the results from its database, while adding it in the cache.
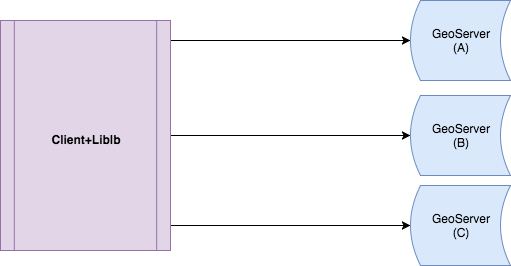
Simulation Architecture
Graphs Explanation
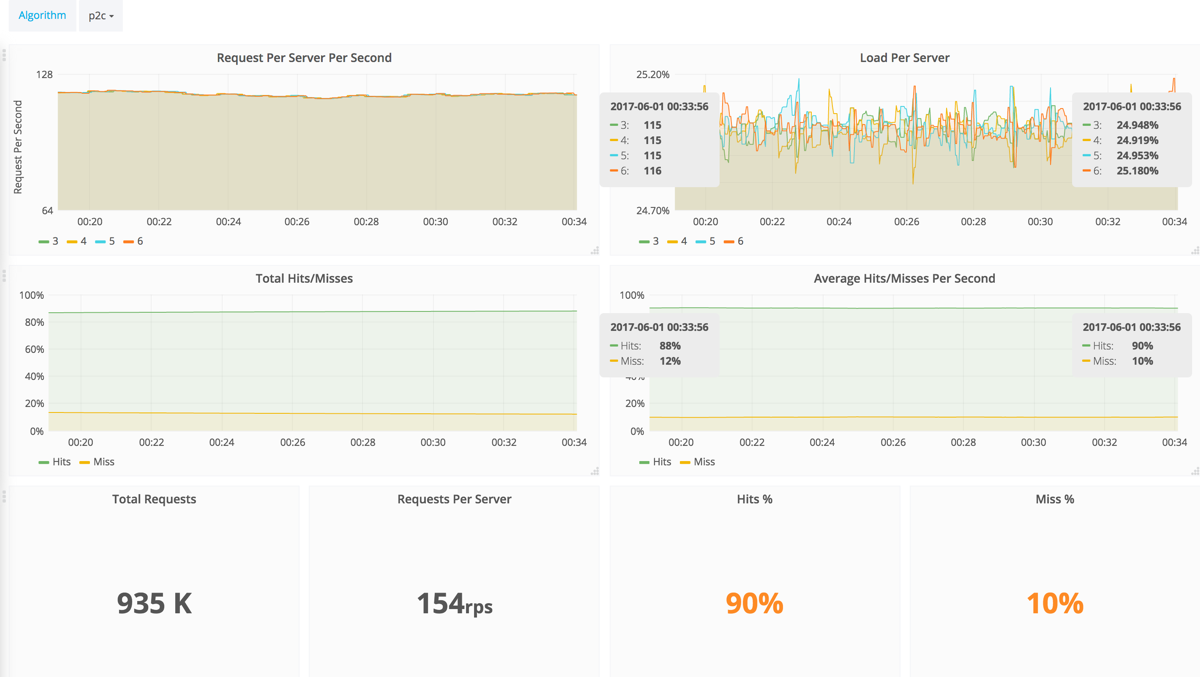
- Request Per Server Per Second: Number of requests processed per GeoServer per second.
- Load Per Server: Load is the percentage of requests sent to every GeoServer in total.
- Total Hits/Misses: Total number of GeoServer cache hits and misses.
- Average Hits/Misses Per Second: Average percentage of the cluster cache hits and misses per second.
- Total Requests: Total number of sent requests to all GeoServers.
- Requests Per Server: Average of total sent requests to a single GeoServer.
- Hits %: Average percentage of the cluster cache hits per second.
- Misses %: Average percentage of the cluster cache misses per second.