Table Of Content What? Experiment Results Strengths Weaknesses Use Cases Further Readings

What is Consistent Hashing?

To understand Consistent Hashing you have to look at the use case it was invented for. In 1997 Akamai had an issue with how to locate a given item in their distributed caching system. There are two ways to accomplish this, the first one is to create a lookup table that maps an item to its server, which require storage that grows as more and more items are added to the cache until it eventually becomes a bottleneck in the system. The second way to map items to their servers is to use a hashing function on the items and use the modular operator to distribute the hashes across the servers hash(item_name) % number_of_server, eliminating the need for a lookup table, and all its shortcomings.

So why did they invent Consistent Hashing?

Well, the issue with modular hashing arises when the number of servers change, items that belonged to specific servers might move to different servers. Exactly number_of_servers / (number_of_servers + 1) of the items get assigned to a different server. For example, in a cluster of 5 servers if you add a 6th server then 83% of the items will move to different servers. A costly operation, just imagine the amount of wasted bandwidth and the sudden increase of load on the servers. In any distributed system, servers come and go very often, especially when using the cloud.

Enter Consistent Hashing

To address the volatile nature of modular hashing, Akamai invented Consistent Hashing, A special kind of hashing that guarantees only 1 / (number_of_servers + 1) of the items move to a new location while everything else stays right where it is.

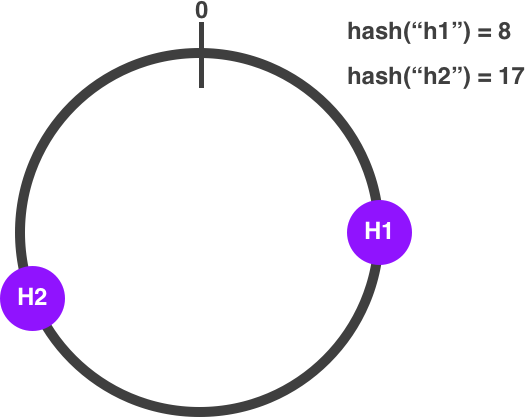
The algorithm works by modeling the keyspace as a circle where the hash function assigns each server to an interval of the circle:

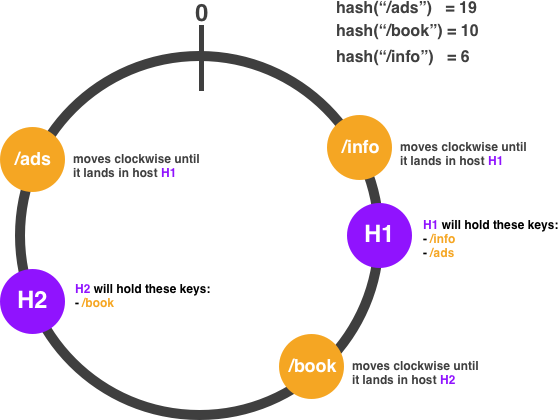
Adding hosts in Consistent Hashing

When we want to know the location of a given item we use the hash function to map it to an interval of the circle and then we walk the circle clockwise until we find a server:

Assigning items to hosts

It works as expected, but one issue with the Consistent Hashing is that it can't guarantee the items to be distributed uniformly between hosts. To address this issue we use a technique called "Virtual Nodes", a fancy name that means instead of adding a single point of a server in the circle, we add N replicas of it. For example:

hostname = "mordor"
number_of_replicas = 10
for i = 0; i < number_of_replicas; i++ {
    h = hash(hostname + i)
    circle.add(h)
}

Client Example

An example of the code used by the client to assign requests to servers, using liblb/consistent Go package, which implements the Consistent Hashing algorithm.

lb := consistent.New("127.0.0.1:8009", "127.0.0.1:8008", "127.0.0.1:8007")
for i := 0; i < 10; i++ {
    host, err := lb.Balance("hello, world!")
    if err != nil {
        log.Fatal(err)
    }
    // all of the work will be assigned to a single hosts
    fmt.Printf("Send request #%d to host %s\n", i, host)
}

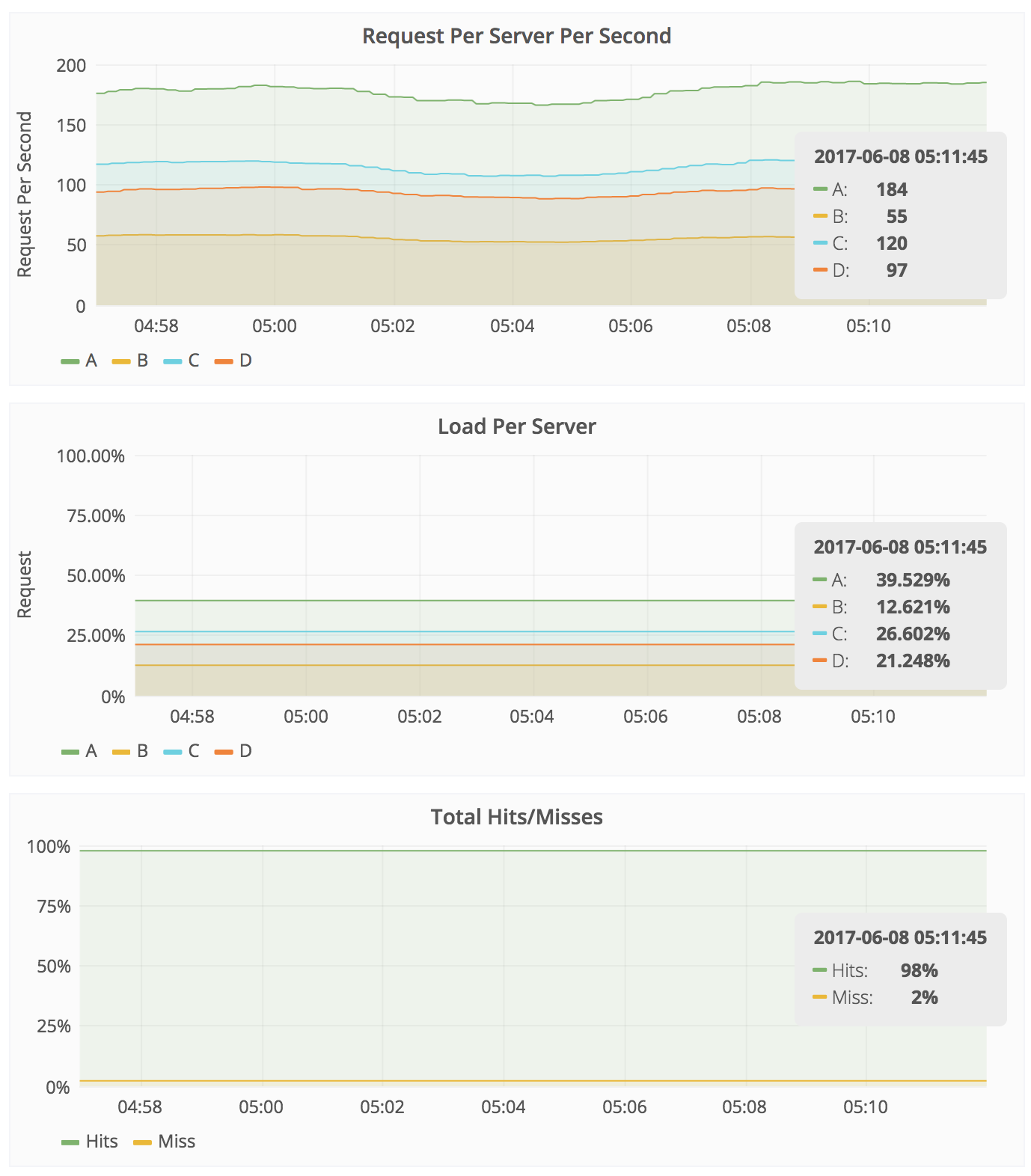
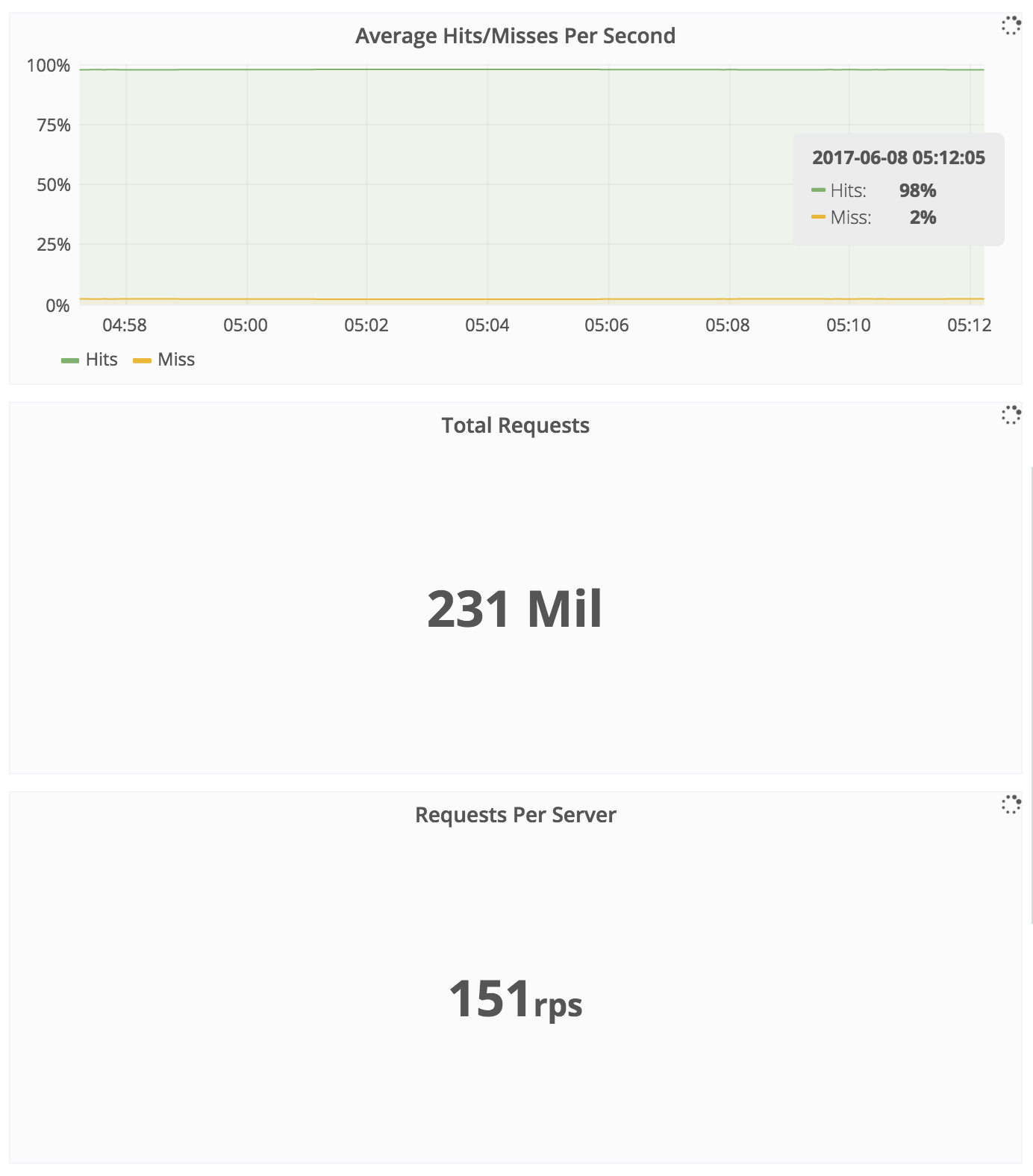
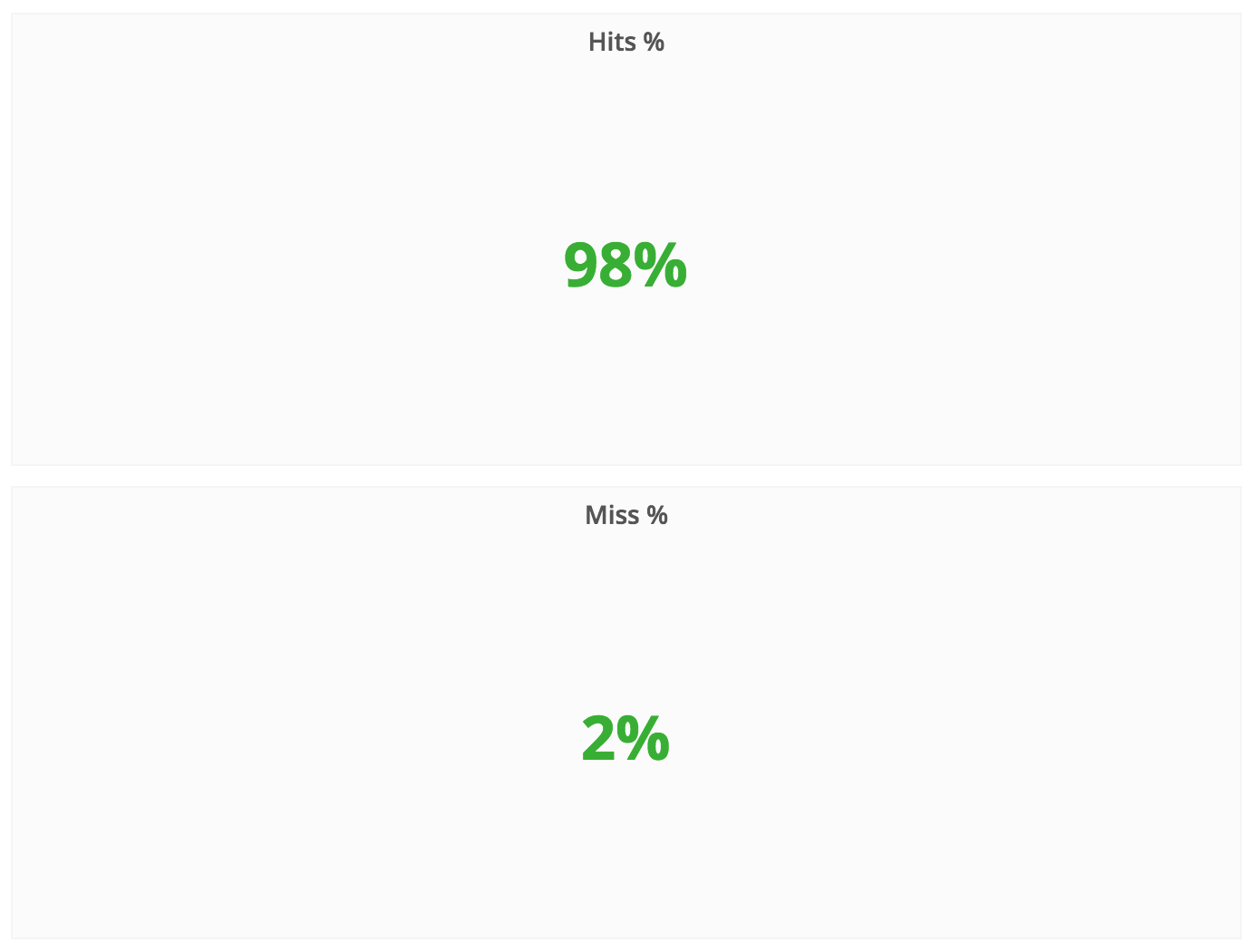
Experiment Results

Consistent Hashing's Experiment Results

For info on the graphs

Strengths

Because of its decentralized nature, nodes don't need to communicate to each other to make a decision on who to assign work to.
Only the list of host is needed to map items to hosts.
Adding or removing a host changes the location of 1 / number_of_servers of the items, which you need to move to their new locations/hosts.

Weaknesses

It provides no bounds over the max load of a host.

Use Cases

Used by Cassandra, DynamoDB, Riak to shard the keyspace between hosts.
Memcached uses it to partition the caches and to route traffic between servers.
Used by Chord as a mechanism to locate items in a Distributed Hash Table.
It basically works great for systems that needs affinity between clients and servers, a websocket load balancer for example.

liblb Consistent Hashing Balancer API docs

GoDoc liblb/consistent

An Empirical Study of Load Balancing Algorithms